Episode 6 : Newton

Nous arrivons au terme de notre cheminement, avec le dernier grand personnage de notre épopée : Isaac Newton.

Nous recroiserons Newton dans la séquence que nous consacrerons aux enjeux proprement philosophiques de la révolution astronomique. Pour cette fois, nous nous contenterons de clore notre périple scientifique, en indiquant en quoi le travail de Newton constitue l'aboutissement de cette grande "révolution" dont nous avons parcouru les étapes.

Pour bien comprendre en quoi a consisté l'apport de Newton à l'histoire de la Révolution astronomique, il faut repartir de la situation telle qu'elle se présentait à lui après Copernic, Tycho Brahé, Kepler et Galilée (auxquels il faudrait ajouter, nous allons le préciser, des penseurs comme Descartes). Quelle est cette situation ?

_ Copernic a posé le principe de l'héliocentrisme

_ Tycho Brahé a montré l'insuffisance des modèles disponibles pour rendre compte des observations (notamment l'orbite de Mars), et il a détruit les orbes des planètes (et, par ricochet, la "sphère des fixes")

_ Kepler a construit le modèle mathématique pemettant de rendre compte du mouvement des planètes du système solaire (avec les 3 lois de Kepler)

_ Galilée a mis en évidence l'immensité de l'Univers, et son homogénéité ; et il a fondé une nouvelle physique (terrestre) selon laquelle le mouvement d'un corps solide était déterminé par la composition des forces qui s'exerçaient sur lui (c'est ce que l'on a appelé ensuite : le "parallélogramme des forces"). Un corps soumis à un mouvement latéral constant, et un mouvement vertical accéléré, parcourait donc une trajectoire parabolique.

Il reste donc un problème de fond, que Kepler a été le premier à poser : comment expliquer le mouvement des planètes dans le système solaire ? Quelles causes peut-on attribuer à ce mouvement ? Pourquoi les planètes tournent-elles selon une orbite elliptique autour du soleil ?

Si Kepler, nous l'avons vu, a été le premier à poser ce problème, c'est qu'avant lui ce problème (pour reprendre la formule d'un grand historien des sciences, Alexandre Koyré) '"était résolu avant même d'être posé" : pour Ptolémée, si les planètes tournaient (en cercles), c'est parce qu'elles étaient fixées sur un orbe qui, lui, tournait du fait d'une impulsion conférée par une "âme" ; et pour Copernic, si les planètes tournaient... c'est que la rotation circulaire était le mouvement naturel d'une sphère. 

Pour Kepler, ces explications sont invalides : il va renoncer progressivement au fait d'accorder une "âme" aux planètes, et il va récuser l'idée de mouvement naturel. Pour Kepler, les astres, comme tous les corps, ont une tendance naturelle à l'inertie. Attention : il faut faire très attention au sens de ce mot. Contrairement au sens du mot "inertie" dans ce que nous appelons aujourd'hui le "principe d'inertie", l'inertie chez Kepler désigne la tendance à l'immobilité. Un corps dans le vide, si on cesse de le pousser, s'arrête (comme nous le verrons, le "principe d'inertie" dit.... exactement le contraire : un corps qui n'est soumis à aucune force conserve éternellement le mouvement qui est le sien). Si, donc, les planètes tournent, c'est qu'une force s'exerce, perpétuellement, sur elles, les "forçant" à avancer.

Nous avons indiqué l'explication donnée par Kepler : le soleil, en tournant sur lui-même, créait une sorte de tourbillon plat, qui entraînait les planètes autour de lui ; et comme la force de ce tourbillon décroissait avec la distance, il était normal que la vitesse des planètes elle aussi, décroisse d'une façon proportionnelle à leur distance au soleil. Par ailleurs, cette force tourbillonaire était doublée d'une seconde force, magnétique cette fois, par laquelle le soleil attirait puis repoussait (comme un aimant) périodiquement les planètes (en fonction de la "face" qu'elles lui présentaient) : d'où leur mouvement elliptique.

Ce système n'aura pas une grande postérité...

Ce qui, en revanche, va avoir beaucoup plus de succès (mais sous une forme modifiée), c'est la réponse que Kepler apportait à un autre problème (qui pour nous, évidemment, est.... le même !), qui était celui de l'attraction que la terre exerçait sur la Lune. Car la terre, pour Kepler, n'était pas comme le soleil : elle ne créait pas de tourbillon plat... Là encore, Kepler va rompre avec toute la tradition issue d'Aristote et de Ptolémée, selon laquelle, si un corps lourd (comme une pomme) "tombe" vers le bas, c'est parce qu'il est animé d'une tendance naturelle à rejoindre le centre du monde (centre de la Terre) ; chez Copernic, ce principe n'était que légèrement modifié : chaque élément tendait à rejoindre le corps qui était apparenté. Ainsi la pomme ou la Lune tendaient à rejoindre la Terre, comme tous les éléments terrestres tendaient à en rejoindre la surface.

Kepler rompt radicalement avec cette tradition en introduisant l'idée selon laquelle, si la Lune reste "accrochée" à la Terre, ce n'est pas parce qu'elle tend vers la Terre, mais parce que la Terre l'attire, et qu'elle attire la Terre en retour. Kepler introduit donc le principe même de la gravité : tous les corps solides s'attirent mutuellement ; plus encore, ils s'attirent proportionnellement à ce que Kepler appelle leur "moles", qui n'est déjà plus la taille mais qui n'est pas encore ce que nous appelons la masse. Donc : la terre et la Lune s'attirent mutuellement, en proporition de leurs moles respectives, si bien que, si aucune autre force ne s'exerçait, elles se rejoindraient, à un endroit situé non pas au milieu, mais en un lieu situé d'autant plus près de la terre que la Terre est plus grosse (a une plus grande moles).

Il est difficile de ne pas voir dans cette explication de l'attraction terrestre l'amorce de la "gravitation" telle que la développera Newton. Oui, mais voilà... Kepler raisonne encore dans un monde où ce qui vaut pour le rapport entre certains corps (La Terre et la Lune) ne vaut pas pour tous les corps, de façon universelle. Les éléments de l'Univers ne sont pas régis par les mêmes lois. Il y a bien une "attraction" de la Lune par la Terre... mais cela ne vaut que parce que ce sont des astres apparentés. Cette attraction ne vaut pas pour le rapport soleil / Terre, et plus généralement pour les corps qui ne sont pas "apparentés".

Pour que l'attraction terrestre puisse être généralisée, et qu'elle devienne un principe universel, selon lequel tous les corps s'attirent mutuellement (proportionnellement à leur masse), il va donc falloir que cette différenciation qualitative de l'Univers, selon lesquels les corps ont des natures différentes (et pas seulement une taille, un poids, un mouvement différents) disparaisse. Il va falloir que l'Univers devienne totalement "homogène", et que les lois qui régissent le rapports entre deux corps valent pour tous les corps de l'Univers.

Cette homogénéisation du monde va se produire sous l'influence d'un courant qui, en lui-meme, n'a pas de lien privilégié avec l'astronomie, qui est le courant "atomiste". Ce courant existait déjà dans l'Antiquité : pour des penseurs comme Démocrite, Epicure ou Lucrèce, le monde était constitué de petites "particules élémentaires", des atomes, dont tout ce qui existe était composé. Ces atomes (il y en avait plusieurs sortes) étaient les plus petits éléments de l'Univers, et toutes les choses de l'Univers étaient constituées (et n'étaient constituées que) d'atomes. Cette idée réapparaît dans la science du XVII° siècle, avec des penseurs comme Gassendi et Boyle. Pour ces deux penseurs, tous les éléments de l'Univers étaient constitués d'atomes, et les atomes étaient les mêmes dans tout l'Univers. Il n'y avait donc pas de différence de "nature" entre les corps, qui étaient tous constitués à partir des mêmes atomes. Le soleil ou les étoiles n'étaient pas d'une "nature" différente de la terre ou de la pomme (même s'ils pouvaient être constitués d'atomes un peu différents).

Si l'on synthétise alors :

     _ le principe d'attraction terrestre, avec le principe selon lequel la force de cette attraction diminue avec la distance

     _ l'homogénité de tout l'Univers (qui permet donc d'étendre l'attraction à tous les corps)

on obtient alors l'idée selon lequel tous les corps de l'Univers (et notamment les astres) s'attirent mutuellement en raison inverse de leur distance.

Cette idée est par exemple énoncée par Hooke, un scientifique contemporain de Newton :

"1° Que tous les corps célestes, sans en excepter aucun, ont une attraction ou une gravitation vers leur propre centre, par laquelle, non seulement ils attirent leurs propres parties et les empêchent de s'écarter, comme nous le vyons de la Terre, mais encore ils attirent tous les autres corps célestes qui sont dans la sphère de leur activité ; que, par conséquent, non seulement le Soleil et la Lune ont une influence sur le corps et le mouvement de la terre, et la terre une influence sur le Soleil et la Lune, mais ausi que Mercure, Vénus, Mars, Jupiter et Saturne ont par leur force attractive une influence considérable sur le mouvement de la Terre, comme aussi l'attraction réciproque de la terre a une influence considérable sur le mouvement de ces planètes.

2° [pour le 2, patientons encore un peu....]

3° Que les forces attractives sont d'autant plus puissantes dans leurs opérations que le corps sur lequel elles agissent est plus près de leur centre."

Les mouvements des planètes doivent donc être expliqués par un principe général selon lequel elles s'attirent mutuellement en proportion de leur distance... nous touchons au but !

Une représentation moderne de Robert Hooke, par Rita Greer

Nous touchons... mais nous n'y sommes pas encore. Car, pour commencer, il faut préciser ce qu'est exactement le rapport mathématique qu'entretiennent la force d'attraction, et la distance entre les corps. On sait déjà que, "plus" les corps s'éloignent, et "plus" l'attraction diminue... mais selon quel rapport mathématique ? On pourrait être tenté d'établir un rapport strictement proportionnel : si on mutiplie la distance par deux, on divise la force par deux, etc. Mais voilà, ça ne va pas : en particulier, cela ne correspond pas au rapport qu'il semble y avoir entre la vitesse des planètes et leur distance au soleil.

La solution du problème, c'est Isaac Newton qui a donnera, en prenant appui sur les lois de Kepler : la force d'attraction n'est pas inversement proportionnelle à la distance : elle est inversement proportionnelle au carré de la distance.

Si un objet A est deux fois plus éloigné qu'un objet B d'un objet C, l'attraction exercée par C sur A ne sera pas deux fois moins grande, elle sera 4 fois (2x2) moins grande. Les planètes sont donc attirées par le soleil "en raison inverse du carré de leur distance".

Sommes-nous parvenus à la fin de notre périple ? Pas tout à fait encore. Car il subsiste un problème : Newton a déduit ce rapport, de façon mathématique, en partant d'orbites circulaires. Or Newton (contrairement à Galilée) l'a appris de Kepler : les orbites ne sont pas circulaires, elles sont elliptiques. Il faut donc à Newton apporter la dernière réponse à la sempiternelle question : pourquoi les planètes tournent-elles autour du Soleil sur des orbites elliptiques ?

Pour comprendre la réponse de Newton, il faut en fait repartir de la dernière "synthèse" newtonienne : celle qu'il opère entre

      1. le principe galiléen de composition des forces (le mouvement d'un corps est la résultante des forces qui agissent sur lui, de leurs "vecteurs")

      2. le principe d'inertie.

Qu'est-ce que ce fameux "principe d'inertie", qui est l'un des fondements de la mécanique moderne ? Pour le comprendre, il faut l'opposer à deux idées fausses :

      1. les corps ont une tendance naturelle au repos : ils ne bougent que si une force s'exerce perpétuellement sur eux : c'était l'idée de Kepler.

      2. les corps sont animés d'un mouvement naturel circulaire : si on les laisse à eux-mêmes, ils tournent en rond : c'était l'idée de Galilée.

Ce sont ces deux idées qui vont être détruites par la mise en lumière du "principe d'inertie", sur lequel repose toute la mécanique moderne, et que l'on peut formuler comme suit :

Un corps sur lequel ne s'exerce aucune force poursuit son mouvement (contre Kepler), et ce mouvement est rectiligne et uniforme (contre Galilée).

En clair, dans l'espace, si une pomme est lancée avec une certaine vitesse dans une certaine direction... elle poursuivra éternellement son mouvement, en ligne droite. Ce principe, ce n'est pas Galilée qui l'a découvert ; ni Kepler ; ni même Newton ; c'est... Descartes, soit l'un des principaux philosophes du XVII° siècle.

René DESCARTES

C'est ici que nous pouvons citer le "2°",que nous avions omis dans la citation précédente :

"2° Que tous les corps qui ont reçu un mouvement simple et direct continuent de se mouvoir en ligne droite, jusqu'à ce que par quelque autre force effective ils en soient détournés et forcés à décrire un cercle, une ellipse ou quelque autre courbe plus compliquée."

Si l'on associe ce principe au mouvement circulaire, on aboutit à la force centrifuge. En effet, si l'on admet qu'un corps, animé d'un certain mouvement, tend à poursuivre ce mouvement en ligne droite, alors il faut admettre qu'un corps que l'on fait tourner autour d'un centre sera animé d'une force qui tend à chaque instant à le "faire sortir" de son orbite ; il suffit de faire tourner une fronde ou un yo-yo pour s'en rendre compte : plus je fais les fais tourner rapidement, plus ils "tirent" sur la corde, et plus ils partiront loin quand je les lâcherai. C'est logique : au moment où je les lâche, ils poursuivent le mouvement qui était le leur au moment où je les ai lâchés, en ligne droite.

Donc, plus je fais tourner un corps rapidement, et plus il tend fortement, à chaque instant, à poursuivre sa route en ligne droite (et donc à "sortr" du cercle) : c'est la force centrifuge. S'il tourne en rond, c'est parce que son mouvement est bien la résultante de deux forces qui s'exercent sur lui : une qui tend à le faire poursuivre sa route en ligne droite (force "inertiale"), une qui le tire vers le centre (la fronde, la ficelle).

Si l'on applique ce principe aux mouvements des astres, on a donc l'idée suivante : comme la pierre au bout de la fronde, si les planètes tournent autour d'un astre (comme la terre autour du Soleil), c'est parce qu'elles sont soumises à deux forces :

     _ la force "centrifuge", qui les projette en ligne droite (vers le lointain)

     _ la force "centripète", qui les ramène vers le soleil (l'attraction). 

Et si le mouvement reste toujours identique (la planète ne s'en va pas dans l'espace, elle ne tombe pas sur le soleil), c'est que les deux forces s'équilibrent. Nous avons bien ici l'explication du mouvement des planètes du système solaire : si elles tournent autour du soleil, c'est parce qu'elles sont à la fois projetées loin de lui (par la force inertiale, centrifuge) et attirées vers lui (par la force d'attraction de la gravité).

[Le paragraphe suivant sera très utile à ceux qui voudraient comprendre dans le détail la solution de Newton au problème du caractère elliptique des orbites. Mais il n'est pas nécessaire pour comprendre l'achèvement de la révolution astronomique. Ceux qui, parmi vous, ne sont pas rebutés par les mathématiques devrairnt le parcourir ; pour les autres.... passez directement à la fin des crochets !

Donc, reprenons : pourquoi ce mouvement est-il elliptique ? Là encore, Newton va trouver la réponse grâce à Kepler : il va en effet constater que la "loi des aires" vaut pour tout mouvement composé d'un mouvement inertial et d'une force d'attraction centrale ; et il montre aussi que, si la force d'attraction est inversement proportionnelle à la distance (comme c'est le cas pour le système solaire), le mouvement qui en résultera sera une "section conique", c'est-à-dire l'une des figures que l'on obtient en "coupant" un cône par un plan. Et l'une de ces sections est... l'ellipse. Et comble de la fortune, dans le cas de l'ellipse la force d'attraction sera orientée vers l'un des foyers : exactement comme c'est le cas en ce qui concerne planètes du système solaire.

 

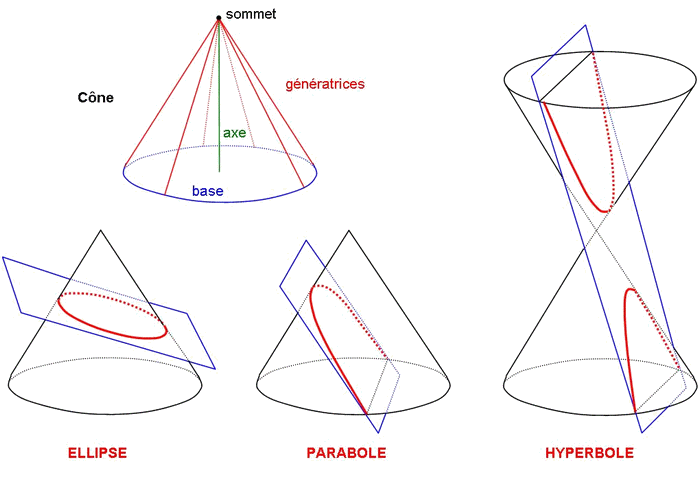
Les différentes "sections coniques"

Pour se représenter comment un mouvement inertial, couplé à une attraction centrale, peut donner lieu à un mouvement elliptique lorsque l'attraction décroît en raison inverse du carré de la distance, on peut faire l'expérience suivante. Si l'on tend un rond de toile d'un mètre de diamètre de façon à obtenir une surface parfaitement plane, et qu'on lance des billes sur la toile, depuis le bord :  le mouvement des billes sera parfaitement rectiligne et uniforme. Les billes seront animées d'un "mouvement inertial" : elles poursuivront leur mouvement à vitesse constante (si l'on fait abstraction des frottements), en ligne droite.

Mais plaçons maintenant, au centre de la toile, une grosse boule de plomb. La boule va déformer la toile, la faire "descendre" en son centre, ce qui va "attirer" les billes qui rouleraient sur la toile. Plus encore, la boule va déformer la toile d'une façon telle que la "dépression" de la toile sera d'autant plus forte que l'on se rapproche de la boule ; plus une bille s'approchera de la boule, et plus elle sera "attirée" par elle au centre de la toile. En fait, l'attraction exercée par le centre de la toile sera; en gros, inversement proportionnelle au carré de la distance. Or quelle va alors être la trajectoire des billes ? Si on lance les billes sur la toile, et si l'on observe leur trajectoire en se plaçant au-dessus de la toile, elles se mettront à tourner autour de la boule de plomb, selon une trajectoire... elliptique.

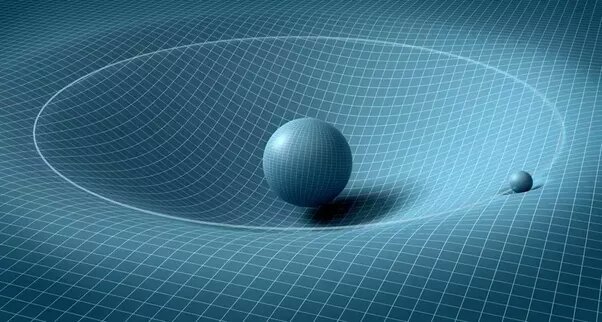
Si on calcule la trajectoire en faisant le bilan des forces, et en faisant abstraction de tous les frottements, on obtiendra tout simplement.... une trajectoire elliptique dont la boule centrale sera l'un des foyers. Et, conformément aux lois de Kepler, la vitesse de la boule sera maximale au point de la courbe le plus proche du foyer (là où la planète est le plus proche du soleil : "périphélie"), et sera minimale au point le plus éloigné ("aphélie").

En fait, on n'obtiendra jamais tout à fait cela, justement parce que sur la toile, contrairement à ce qu'il se passe dans le vide spatial, il y a des frottements : ce qui va faire dévier la trajectoire de la boule à chaque passage à proximité de la boule centrale. On obtiendra donc, en vérité, une trajectoire de ce type :

J'emprunte cette image à une page web très intéressante . On reconnaît ici les courbes elliptiques (déviées par les frottements), dont le centre est l'un des foyers

Newton a donc, enfin, répondu à la question de Kepler : à la question de savoir pourquoi les planètes tournaient autour du soleil, et sur une orbite elliptique, il a donné la réponse définitive. Les planètes du système solaire tournent autour du soleil selon une trajectoire elliptique parce que cette trajectoire résulte mathématiquement de la déflation d'un mouvement inertial par une attraction centrale, due à la force d'attraction gravitationnelle dont la force est en raison inverse du carré de la distance.

Mais Newton va faire bien plus encore : en comparant la force d'attraction que le soleil exerce sur les planètes, la force que la terre exerce sur la Lune, et la force que la Terre exerce sur les corps (comme une pomme qui tombe sur le sol), il va montrer que cette force est toujours la même. La force d'attraction gravitationnelle est constante : qu'elle s'exerce du soleil sur les planètes (et réciproquement), de la terre sur la Lune (et réciproquement), de la Terre sur la pomme qui tombe... il s'agit bien de la même force, toujours identique à elle-même.

Une illustration par Gotlib de la légende selon laquelle Newton aurait trouvé sa loi de la gravitation universelle en regardant tomber une pomme.

Newton a donc définitivement aboli la distinction entre physique céleste et physique terrestre : l'ensemble de l'Univers est bien régi par une seule et même force, identique dans l'ensemble de l'Univers, identique pour l'ensemble des corps : TOUS les corps de l'univers s'attirent réciproquement en raison inverse du carré de leur distance.

La gravitation est la force qui régit les mouvements des corps de l'ensemble de l'Univers : le principe newtonien est bien celui de la gravitation universelle.

Le grand oeuvre de Newton : les Principia Mathematica : 1687.

Newton a donc unifié la science : la physique terrestre et la physique céleste ne forment plus qu'une seule et même physique universelle ; ce qui implique que l'Univers, lui aussi, se trouve unifié, d'une unité qui n'a plus rien de commun avec l'unité du "cosmos" de Ptolémée. L'Univers est désormais unifié par le fait qu'il est régi par un même principe qui gouverne tous les corps, de l'atome aux étoiles, ainsi soumis aux même lois. Ce qui fait l'unité de l'Univers, c'est la soumission de tous ses constituants aux mêmes principes physiques, et donc aux mêmes lois mathématiques.