Episode 4 : Kepler

Nous avons montré dans les épisodes précédents comment l'image de l'univers telle qu'elle avait été construite par Ptolémée rencontrait des objections de plus en plus fortes, aussi bien dans sa prétention à la vérité que dans sa capacité à rendre compte des observations. Le grand problème, c'est qu'on ne disposait d'aucun système de remplacement : le système de Copernic, nous l'avons vu n'était guère satisfaisant, et Tycho, en élévant considérablement le niveau de précision des observations, n'avait rendu que plus criant l'écart indubitable entre la position des astres dans le ciel et les prévisions théoriques, même dans son propre système (géo-héliocentrique). En particulier, l'orbite de Mars résistait à toutes les tentatives d'intégration dans les modèles théoriques. C'est pourquoi Tycho Brahé va décider de la confier à un astronome encore peu connu mais qui s'avèrera être l'astronome le plus génial qui soit : Johannes Kepler.

Le plus fascinant, le plus sympathique, le plus génial des astronomes du XVII° siècle

Au moment où se voit chargé de traiter l'orbite de Mars, Kepler est déjà un astronome aguerri. En fait, il dispose déjà des deux principes qui vont lui permettre d'opérer le tournant décisif dans l'histoire de l'astronomie :

     a. Il est copernicien : sa conviction est frermement établie, le soleil doit être au centre du système solaire. Et pas seulement parce qu'il est la "lampe" de l'univers, ou parce que cela permet de simplifier les équations. Pour Kepler, c'est bien en vérité que le soleil est au centre, et il l'est principalement du fait de considérations physiques. Pour Kepler, c'est bien le soleil qui dispose de la puissance suffisante pour faire tourner les astres autour de lui (Kepler n'abandonnera jamais l'idée selon laquelle c'est le soleil qui agit comme une force sur les planètes qui l'entourent).

Cette idée peut nous sembler, aujourd'hui, inappropriée ; elle révèle néanmoins un changement de perspective très important dans la manière considère l'astronomie. Pour lui, il ne s'agit pas seulement de produire un système mathématique qui corresponde aux observations, qui sauve les phénomènes (même à le considérer, du fait de cette correspondance, comme "vrai"). Pour lui, le système théorique doit reprendre à son compte la caractéristique essentielle de ce qui constituait le "système 1" de Ptolémée en tant que système "vrai" : il doit être compréhensible. C'est-à-dire qu'il ne doit pas seulement donner une description mathématique des mouvements des planètes : il doit également donner l'explication de ce mouvement, il doit permettre de comprendre pourquoi les planètes effectuent ce mouvement, et pas un autre.

Ce que Kepler veut construire, c'est bien une physique des cieux : un système qui nous explique comment les planètes bougent et pourquoi elles le font : un système qui nous permette de comprendre l'univers (et de rendre compte de ses mouvements). En ce sens, Kepler est beaucoup plus qu'un astronome du XVII° siècle : c'est l'inventeur de l'astrophysique.

Pour Kepler, ce n'est pas parce que le sysème correspond aux observations qu'il est vrai : c'est parce qu'il est vrai qu'il doit, par conséquent, correspondre aux observations. Chose d'autant plus difficile à faire que Copernic, contrairement à Galilée, va abandonner le vieux principe "explicatif" hérité d'Aristote : si une sphère tourne en rond, c'est bien normal : c'est son mouvement naturel !

     b. Le second principe fondamental de la démarche de Kepler est également déjà inscrit dans son travail : Kepler est absolument convaincu que l'univers est régi par des lois mathématiques. Tel est le principe qui permet de dépasser l'opposition entre, d'un côté, ce qui est "vrai" et, de l'autre, ce qui permet de rendre compte, mathématiquement, des observations. Pour Kepler, les mathématiques ne sont pas seulement un outil dont l'homme dispose pour dessiner des régularités dans les phénomènes. Les équations mathématiques ne sont pas des constructions que l'homme projette sur les phénomènes : la réalité EST mathématique, elle a été conçue de façon mathématique par un Dieu mathématicien. En construisant les équations qui correspondent au mouvement des astres, l'astronome ne "projette" donc pas des formules sur la réalité, il ne fait que retrouver les lois que Dieu lui-même leur a imposées.

Un physicien "keplérien" du XX° siècle : Paul Dirac

Nous reviendrons sur ce point-clé par la suite. Mais il permet déjà d'expliquer pourquoi, selon Kepler, ll doit être possible de trouver le modèle mathématique correspondant aux observations, et que le modèle mathématique qui le fera sera le modèle vrai, celui qui correspond au modèle suivi par Dieu lui-même dans sa Création. Et l'astronome qui le fera sera le grand témoin de la Sagesse de Dieu qui, dans sa création, n'a évidemment rien fait au hasard, mais l'a entièrement soumise à la rationalité mathématique.

C'est ce second principe que Kepler a mis en oeuvre dans sa première oeuvre, le Mysterium Cosmographicum (le "Secret du Monde"), dans lequel il soutenait que le système solaire est fondé sur la succession des solides réguliers. Sans entrer dans les détails du texte de Kepler, l'idée fondamentale est assez simple : chaque planète du système solaire suit un cercle qui correspond à l'un des cinq polyèdres réguliers (un polyèdre régulier est une structure dont toutes les faces sont identiques, de même que ses angles ; au XVII° siècle, on n'en connaît que 5) qui lui correspond. En gros, si l'on dessine un cube (qui est un polyèdre régulier), on peut placer dans ce cube une sphère, qui s'y ajuste parfaitement ; dans le système de Kepler, la trajectoire de Jupiter correspond à un déplacement sur cette sphère ; mais on peut aussi placer le cube lui-même dans une autre sphère (plus grande), qui s'y ajuste parfaitement ; cette fois, c'est la trajectoire de Saturne qui correspondrait à un déplacement sur cette sphère.

Les "sphères" correspondent donc aux anciennes "orbes" de Copernic : sauf qu'il ne s'agit plus de sphères réelles, cristallines ou non : ce sont de pures réalités mathématiques, qui nous expliquent pourquoi Dieu a conçu l'univers de cette façon, la "logique" qu'il a suivie pour déterminer la trajectoire des planètes. Même le nombre des planètes du système solaire devient mathématiquement logique : avec le principe mis en lumière par Kepler, avec n polyèdres réguliers, on peut placer n + 1 planètes ; or combien y a-t-il de polyèdres réguliers ? 5. Et combien y a-t-il de planètes ? 6. Si Dieu a placé 6 planètes dans le système solaire, c'est parce que c'est le nombre qui correspond à la succession des polyèdres réguliers. Oui, décidement, Dieu est bien un mathématicien.

Cette belle construction, Kepler n'y renoncera jamais totalement, même s'il la transformera radicalement. Mais au moment où il rejoint Tycho Brahé, ce magnifique système, comme tous les autres, souffre d'un défaut que Kepler n'arrive pas à résorber : il ne "colle" pas de façon satisfaisante avec les observations... et notamment (décidément !) avec l'orbite de Mars telle qu'on l'observe dans le ciel. Quand Kepler rejoint Tycho, il en est certain : avec le trésor des observations réunies par l'astronome Danois, il va être possible de trouver l'équation mathématique correspondant en tout point à la trajectoire des planètes (même Mars) : de trouver, donc, les vraies équations : celles que Dieu a suivies dans sa Création.

Et, de fait, la collaboration avec Tycho, puis, après la mort de ce dernier, le travail sur ses observations (que Kepler, contrairement à Tycho, va s'empresser de publier), vont mener Kepler très loin dans la mathématisation de l'Univers... mais d'une manière assez différente de ce qu'il avait supposé.

Nos n'entrerons pas ici dans le détail des recherches de Kepler (mais nous reviendrons en revanche sur le "style" littéraire qu'il adopta pour nous les raconter). Nous nous bornerons à indiquer les trois grands résultats auxquels il est parvenu. Ces résultats, ce sont les trois "lois de Kepler", que tous les astronomes connaissent. Pour des raisons pédagogiques, je les prends dans l'ordre inverse :

     a. la troisième loi établit la correspondance mathématique entre le temps qu'une planète met à parcourir toute la trajectoire qu'elle dessine autour du soleil, et sa distance au soleil. Plus une planète est distante au soleil, moins elle va vite, et plus la distance qu'elle a à parcourir est grande : donc plus elle met de temps à opérer sa révolution. La première loi établit le rapport mathématique entre la distance au soleil et le temps de révolution.

     b. La deuxième loi, dite "loi des aires", établit le rapport mathématique entre la vitesse de la planète et sa position. Car Kepler va devoir abandonner un principe-clé de l'astronomie ptoléméenne : la vitesse des planètes n'est pas constante. Elle varie en fonction de leur position sur leur orbite. Mais selon quelle loi ? La seconde loi énonce que la vitesse de la planète est telle que, à n'importe quel moment, elle balaiera des aires égales en des temps égaux. Imaginons que la planète soit reliée par un cordon au centre de son orbite. Entre l'instant t, et un instant t + n (une seconde, une minute, un mois...), le cordon va "balayer" une certaine surface. La seconde loi énonce que, à n'importe quel moment, la surface balayée pendant un temps déterminé (minute, heure, jour, mois...) sera toujours identique.

Bien évidemment, cette loi n'aurait pas grand intérêt si la trajectoire des planètes était strictement circulaire : si je fais tourner un yo-yo autour de ma main, il est évident que le cordon du yo-yoi balaiera la même surface pendant une seconde, que le yo-yo soit en bas, en haut ou sur le côté. Justement parce que :

     _ la vitesse du Yo-Yo est constante,

     _ sa trajectoitre est circulaire

     _ ma main est au centre du cercle.

On peut donc considérer le mouvement du Yo-Yo comme un mouvement circulaire uniforme.

Mais justement, ces trois affirmations sont détruites par la première loi... la plus révolutionnaire, celle que Kepler n'a adoptée que lorsque, réellement, il aura épuisé toutes les hypothèses qui permettraient de l'éviter. Et ce qui va à la fois conduire et contraindre Kepler à cette première loi, c'est bien sûr... l'orbite de Mars !

     c. La première loi de Kepler est la plus simple à formuler : la trajectoire des planètes du système solaire n'est pas un cercle dont le soleil serait le centre, mais une ellipse dont le soleil est l'un des foyers !

Pour comprendre ce qu'est une ellipse, il suffit de se mdemander comment on peut en construire une avec une ficelle; deux clous et un crayon :

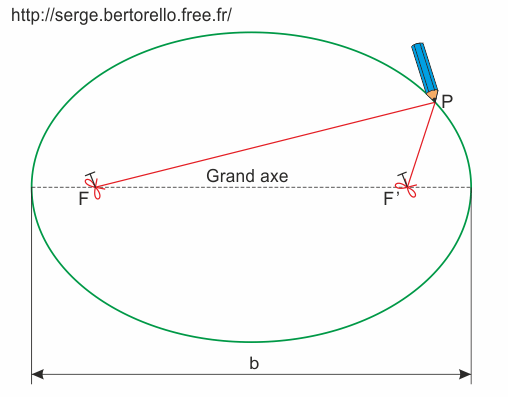
Et par conséquent, si on place le soleil: à l'un des centres, et que l'on remplace le crayon par une planète, ça donne ça :

 

On comprend alors ce que signifie la deuxième loi : la vitesse de rotation de la planète n'est pas constante, mais la surface qu'elle balaye si on la rattache au soleil est, elle, constante, quelle que soit sa position. En un même temps (disons, une semaine), la planète parcourera une surface moins allongée, mais plus large si elle est proche du soleil (elle va plus vite) ; elle parcourera une surface plus allongée, mais moins large, si elle est éloignée du soleil (elle va moins vite). Pour rependre une dernière illustration au site de Serge Bertorello (que je remercie au passage) :

 

On a du mal à mesurer aujourd'hui la force qu'il a fallu à Kepler pour renoncer à un principe aussi profondément inscrit dans la pensée occidentale depuis l'Antiquité, et donc dans l'astronomie : la perfection du cercle. Dans le système de Kepler, il continue bien y avoir un "centre" (il s'agit boien d'un système héliocentrique), mais ce centre n'est plus le centre d'un cercle, la trajectoire des planètes n'est plus circulaire. Kepler lui-même n'a renoncé que la mort dans l'âme au principe d'une orbite elliptique. Et il ne l'a fait, cette fois encore, que sous la contrainte de deux principes :

     a. l'univers est régi par des lois mathématiques : l'orbite des planètes doit donc être modélisable par une équation

     b. l'équation mathématique doit correspondre aux observations

Kepler devait donc trouver une formulation du mouvement des planètes, qui soit à la fois mathématiquement valide et en accord avec les observations. Or la seule formule qui satisfasse ces deux exigences : c'est la formule de l'elllipse. Et l'on comprend alors pourquoi c'est Mars qui posait le problème insoluble, et pourquoi c'est son étude qui a conduit Kepler à identidier le vrai mouvement des planètes : Mars a l'orbite la plus elliptique de tout le système solaire. Il était donc impossible de faire "rentrer" sa trajectoire dans un cercle. Mais désormais Mars est dompté, vaincu : il n'est plus cet astre fou qui n'en faisait qu'à sa tête, et dont les mouvements capiricieux se refusaient à tout ordre, à toute loi ; l'astronome Kepler l'a rapatrié dans l'ordre mathématique, lui assignant sa place dans le système rationel de la création, l'enchaînant défintivement à son orbite elliptique.

Kepler a renouvelé l'exploit de Vulcain : capturer Mars dans ses filets (tableau de Paris Bordone, XVI° siècle)

Avec Kepler, c'est la distinction entre "système 1" et "système 2" qui disparaît définitivement. Il n'y a plus, d'un côté, un système "vrai" (correspondant au monde tel qu'il est en réalité, et compréhensible), et de l'autre un système permettant de "sauver les phénomènes" (en construisant des modèles mathématiques permettant de situer et de prévoir la position apparente des astres dans le ciel). Il n'y a qu'un seul et même système : un système mathématique qui est à la fois :

     a. le système  vrai, celui qui correspond à la réalité telle qu'elle a été conçue par Dieu, qui est le plus grand des mathématiciens

     b. le système qui correspond aux observations, qui "sauve les phénomènes"

Mais ce système est bien loin de celui de Ptolémée, dont tous les principes ont été détruits :

     a. le système n'est plus géocentrique, mais héliocentrique ; même le "centre" de l'Univers n'est en fait qu'un foyer d'ellipse

     b. la trajectoire des planètes n'y est plus circulaire, leur vitesse n'est plus constante

     c. il n'y a plus "d'orbes" sur lesquels seraient fixées les planètes ; ce qui remet en cause par ricochet l'existence d'une "sphère des fixes" à laquelle seraient rivées les étoiles... et donc la clôture de l'univers.

Les fractales : ou comment, pour faire apparaître l'ordre mathématique de l'Univers, il faut d'abord en admettre le chaos apparent...

Reste alors une question. Si le système du monde tel que Kepler l'a construit est bien le vrai, il doit donc être possible de l'expliquer et de le comprendre. Il reste donc à expliquer pourquoi les planètes tournent ainsi autour du soleil, et pourquoi leur mouvement est elliptique. Quelle explication physique peut-on donner à cette trajectoire ?

Pour répondre à cette question, Kepler va construire un système physique assez complexe, sur lequel nous ne nous étendrons pas ici, car il n'est pas nécessaire pour comprendre la suite de l'histoire de la révolution astronomique. En gros, pour Kepler, le soleil agit comme une sorte d'aimant qui, en tournant sur lui-même, fait se mouvoir les planètes autour de lui. Et si la trajectoire des planètes est elliptique, c'est parce que tout en les animant, le soleil les attire et les repousse tour à tour. Les planètes n'ont donc pas de mouvement spontané, "naturel" : elles sont mues par la force qui réside dans le soleil.

Le point important est qu'il s'agit bien ici d'une physique des cieux : Kepler cherche à mettre en lumière une explication physique, mécanique, du mouvement des planètes, qui permet de comprendre pourquoi les planètes rournent autour du soleil. C'est ce même projet qui animera Newton, et que ce dernier portera à son point d'aboutissement, en donnant la raison physique de l'orbite des planètes : la gravitation universelle. Mais nous n'en sommes pas encore là.

Les effes de l'aimant sur l'émail de fer... une structure très astronomique

Il resterait encore beaucoup de choses à dire sur Kepler. Mais comme elles ne sont pas nécessaires pour comprendre la transformation de l'image de l'Univers qui s'opère dans la "révolution astronomique", nous les laisserons de côté. Par exemple, Kepler rattachera dans sa dernière oeuvre, L'harmonie du monde, la nature mathématique du mouvement des planètes à des considérations musicales. A chaque

Pour nous, ce lien entre mathématiques et musique peut sembler curieux. Il ne fait en fait que renouer avec une idée très ancienne : dans l'Antiquité grecque, le maître de "musique" enseignait surtout des principes mathématiques, ce qui correspond à une réalité : la musique est une affaire de mathématiques. Par exemple, si on tend fermement une corde (par exemple, une corde de guitare), et que l'on gratte la corde, on entend une certaine note. Mais si l'on place son doigt à la moitié de la corde en question, on entendra une autre note, qui correspond à l'octave de la première (si la première note était un "do", la seconde sera un autre "do", plus aigu). De même, si l'on place le doigt au tiers de la corde, on obtiendra la quinte (un "sol"), soit une note dont la fréquence est trois fois supérieure à la première, etc. Pour visualiser en quoi la position des doigts sur la corde correspondant à l'échelle des slons, il suffit de jeter un oeil aux frêtes d'une guitare : à chaque "fraction" de la corde correspond une note déterminée.

 

Pour Kepler, on peut donc faire correspondre à chaque planète du système solaire une certaine mélodie, comme si l'on suivait avec le doigt humide la trajectoire d'une planète sur une coupe de cristal ellptique (selon le vieux principe de l'orgue de verre) ; aux variations de la vitesse de l'astre correspondrait des variations du son, faisant ainsi correspondre à chaque planète une mélodie propre. De sorte que le système solaire devient une sorte d'orchestre, dans lequel chaque planète produit sa mélodie : on retrouve ici la très vieille idée astronomique de la "musique des sphères", que l'homme ne peut pas entendre, mais qui constitue le concert que Dieu se joue à lui-même à travers sa création. Le Dieu de Kepler n'est pas seulement un dieu mathématicien : c'est ausi un dieu musicien, qui a conçu l'univers comme un spectacle, et comme un spectacle musical. La beauté de l'univers tient à son harmonie : or ce qui est harmonieux, c'est à la fois ce qui est mathématiquement parfait, régulier, et ce qui est esthétiquement réussi. Pour Kepler, la beauté mathématique de l'univers (en tant que système d'équations parfaitement cohérentes) est le reflet de sa beauté musicale.

Oui, l'Univers est un spectacle : pour les yeux (de celui qui contemple ses mouvements harmonieux), pour l'intelligence (du mathématicien), et pour l'oreille de Dieu. En mettant en lumière les rapports mathématiques qui régissent l'Univers, l'astronome célèbre donc la gloire de Dieu, en dévoilant à la fois la rationalité et la beauté de l'Univers qu'il a conçu. C'est ce qui explique le caractère à la fois fascinant et déconcernant de la dernière oeuvre de Kepler, où s'entremêlent considérations astronomiques, calculs mathématiques, partitions musicales... et hymne au Créateur.

Lorsque l'on reprochait à Lénoard de Vinci de peindre le dimanche, jour de repos du Seigneur, il répondait que sa peinture était une prière : en manifestant la beauté de la création, le peintre célébrait la gloire du Créateur ; nul doute que, pour Kepler, le travail de l'astronome s'apparentait à une prière... chantée par un choeur de mathématiciens !