Révolution cartographique 2

La terre... début d'un cours d'astronomie, ou de géographie ?

Dans la séquence précédente, nous avons montré comment la révolution cartographique s'inscrivait dans le processus global d'une révolution culturelle ; portée par la dynamique qui conduisait à une vision du monde à caractère scientifique, la géographie s'est constituée comme discipline à part entière en devenant une science ; en tant que science, elle a donc produit des images scientifiques du monde, qui ont à leur tour contribué à l'élaboration d'une vision du monde scientifique. 

Mais si la géographie a pu jouer ce rôle, c'est précisément parce qu'elle n'est pas un domaine indépendant et autonome : elle est liée à tous les autres espaces du savoir, dont elle répercute les évolutions, et qu'elle contribue elle-même à façonner. La géographie joue donc le rôle d'interface dynamique entre les différents champs du savoir, qui l'influencent et qu'elle influence. C'est ce que nous allons approfondir aujourd'hui.

I. Géographie, astronomie et mathématiques

     A. Géographie et astronomie : la cosmographie

Nous l'avons dit, le premier domaine avec lequel la géographie est en interaction est l'astronomie. Si l'autonomisation de la géographie va donner à cette discipline une consistance propre, elle ne remettra pas en cause son rapport à l'astronomie, qu'elle va au contraire contribuer à approfondir : on pourrait même dire que jamais l'astronomie et la géographie n'auront été aussi liées qu'aux XVI° et XVII° siècle.

Le rapport entre la géographie, comme étude de la terre, et l'astronomie est assez évident. Il ne viendrait pas à l'esprit d'un scientifique d'aujourd'hui de dissocier l'étude des particularités de l'atome, et l'étude de ses interactions avec les autres constituants de la matière, ou avec les autres atomes au sein des molécules ; de la même façon, il semblait étrange à un scientifique de la Renaissance de dissocier l'étude du globe terrestre de l'étude de son interaction avec les autres planètes. La géographie apparaissait ainsi comme une sous-partie du vaste ensemble de l'astronomie.

Cette association apparaît très clairement dans la forme des (innombrables) traités qui viseront à présenter les avancées du savoir dans les domaines conjoints de l'astronomie et de la géographie ; ces traités, dont les premiers datent du XIII° siècle, étaient résumés sous le titre englobant de "Traité de la sphère". On ne compte plus les "traités de la sphère" qui seront publiés en Europe, et qui rencontreront un succès jamais démenti (un des premiers d'entre eux, celui de Sacrobosco au XIII° siècle, connaîtra près de 400 éditions !). Or ces traités de la sphère étaient indiscinctement des exposés de géographie (étude du globe terrestre, rotondité, matière, etc.) et d'astronomie (orbites et mouvement des planètes, explication des éclipses, etc.). Il est d'ailleurs parfois difficile de déterminer si la "sphère" dont il s'agit est la Terre, ou la sphère des fixes englobant l'univers. Ce lien entre géographie et astronomie apparaît également dans le nom par lequel on désignait le spécialiste de l'étude du globe terrestre : non pas le géographe, mais le "cosmographe".

Existait donc un triptyque constitué des domaines de l'astrologie (description de l'univers, et de la place de la terre dans l'Univers), de la cosmographie (description du globe terrestre) et de la "chorographie" (étude d'une région particulière du monde terrestre) : ces domaines ne correspondaient ainsi qu'à des différences "d'échelle".

Les traités "De la sphère" constitueront jusqu'à la fin du XVIII° siècle le principal support pédagogique pour l'apprentissage de la géographie-astronomie au sein des écoles (celui-ci date de 1790).

     B. Géographie, astronomie et mathématiques : la géométrisation de l'espace terrestre

Cette interdépendance entre géographie et astronomie ne sera pas remise en cause, nous l'avons dit, par l'accès de la géographie au statut de science. Au contraire, c'est précisément par sa corrélation avec l'astronomie que la géographie va pouvoir émettre ses prétentions à la valeur scientifique, en soumettant la représentation du globe terrestre à un principe géométrique, fondé sur des coordonnées : latitude (axe Nord / Sud) et longitude (axe Est / Ouest). De façon curieuse, si la Révolution astronomique va essentiellement se constituer contre l'image du monde construite par Ptolémée au II° siècle, la Révolution cartographique va en partie reposer sur la redécouverte de Ptolémée à partir du XIV° siècle. Car Ptolémée n'était pas seulement le plus "astronome" de l'Antiquité : c'en était aussi le plus grand géographe, et plus précisément le plus grand cartographe.

          1. Géométrisation et coordonnées

L'histoire ne nous a pas permis de conserver de cartes réalisées par Ptolémée ; mais elle a néanmoins conservé les grands traités de Ptolémée relatifs à cette question, et notamment la Géographie. Et dans la mesure où l'un des buts de Ptolémée était justement de donner les principes et les règles (notamment mathématiques) que l'on devait suivre pour la construction de ces cartes, il est possible de les reconstituer à partir de ses oeuvres, comme l'ont fait les cartographes de la Renaissance. Voici la plus célèbre d'entre elles, la carte de l'Oecoumène (monde habité) :

Et en voici une autre, de la Scandinavie :

Il n'est guère besoin d'être cartographe de profession pour voir que ces cartes du second siècle de notre ère se rapprochent beaucoup plus de ce que nous considérons comme une "carte" que les fameuses cartes "T dans l'O" de l'époque médiévale. C'est que le projet de Ptolémée était beaucoup plus proche du nôtre : son but était bien de proposer une image du monde qui n'avait rien de symbolique, mais qui visait à situer chaque terriroire à sa place, en respectant les contours et les distances, dans l'espace global du monde habité. Et pour ce faire, Ptolémée avait introduit ce qui allait devenir le principe fondamental de la cartographie moderne : la géométrisation de l'espace terrestre, selon l'axe double de la distance à l'équateur (latitude) et à un méridien d'origine (longitude), qu'il situait pour sa part dans les "îles des bienheureux" (les Canaries). Dans le livre I de la Géographie, Ptolémée expose les difficultés posées par le cacul des latitudes et (surtout) des longitudes ; et dans les livres II à VII, il fournit des listes topographiques et attribue des coordonnées de 8 000 endroits d'Europe, d'Asie et d'Afrique.

Ptolémée n'était pas le premier à avoir adopté ce principe des coordonnées géométriques ; elle provient au moins d'Erathostène (3e siècle av. J-C), et avait été mise en oeuvre par Hipparque (2e siècle av. JC) ; mais c'est bien à travers Ptolémée que les cartographes de la Renaissance vont à leur tour "redécouvrir" la description géométrique du globe terrestre.

          2. Géographie et projection

Mais plus encore, c'est chez Ptolémée qu'ils vont trouver les principes mathématiques permettant d'apporter des solutions satisfaisantes au problème-clé des cartographes : représenter sur une carte (et donc sur un espace plan) un monde sphérique. C'est chez Ptolémée que les Humanistes vont trouver les règles mathématiques permettant de produire des "projections" de la sphère sur le plan, avec une discussion portant sur les avantages et inconvénients de diverses solutions possibles.

Ainsi, Ptolémée décrit deux méthodes mathématiques de projection pouvant être utilisées pour réaliser une carte générale de l'écoumène. La première, plus simple, est essentiellement une projection conique, dans laquelle les parallèles sont représentés avec des cercles concentriques et les méridiens avec des droites qui convergent vers un même point unique.

La carte (reconstituée) de l'oecoumène réalisée par Ptolémée avec projection conique

Le problème de ce système de projection, c'est qu'il tend cependant à représenter les parallèles avec des arcs qui s'agrandissent de plus en plus quand on va vers le Sud ; alors qu'à partir de l'équateur, la longueur réelle diminue : il suffit de jeter un oeil sur un globe pour voir que les parallèles, de part et d'autre de l'équateur, sont de plus en plus petits (l'équateur est le "plus grand" des cercles parallèles)

Ptolémée a donc proposé de "corriger" ce défaut en "inversant" l'orientation des méridiens au Sud de l'équateur, de façon telle que le méridien le plus au Sud ait la même longueur que son symétrique. Comme l'essentiel de l'oeucoumène est situé au Nord de l'équateur, la partie "inversée" n'a d'ailleurs pas besoin d'être très étendue.

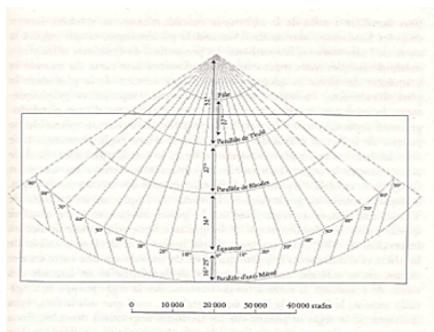
Mais Ptolémée préférait en fait une troisième méthode de projection, un peu plus complexe. Il s'agit de représenter les méridiens (donc les axes Nord-Sud), non avec des segments de droite mais avec des arcs, de sorte que seul le méridien central (le méridien de référence) prenne la forme d'une droite. Les parallèles prennent également la forme d'arcs (concentriques). Cela nous donne une structure géométrique qui apparait clairement ci-dessous.

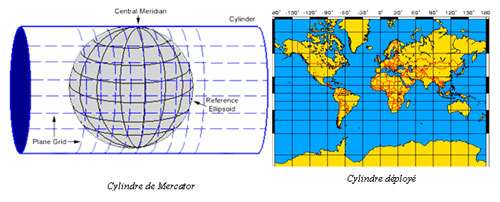
C'est cette méthode de projection qui est mise en oeuvre dans la carte de l'écoumène dont nous étions partis. Et pour les cartes régionales, Ptolémée mobilise une quatrième méthode, qu'il emprunte à Marinos de Tyr : il s'agit d'une projection cylindrique, dans laquelle les méridiens et les parallèles forment une grille de lignes droites qui se coupent à angle droit ; cette méthode produit des distorsions énormes à grande échelle quand on s'approche des pôles. En effet, le principe de la représentation cylindrique est de s'imaginer que l'on projette une image sur un cylindre... et que l'on "déploie" ensuite le cylindre. Cela a pour principal effet de grandir de plus en plus les territoires quand on s'approche des pôles, à la fois en hauteur (puisque les parallèles vont s'éloigner du fait du "redressement" du clylindre) ET en largeur (puisque, pour rendre les méridiens parallèles, on va devoir "tirer" sur le haut et le bas de la carte pour donner aux pôles la même "largeur" que l'équateur).

En gros, il faut s'imaginer que vous projetez une image de la terre sur un cylindre photographique, que vous aplatissez ensuite le cylindre, puis le tordez suffisamment pour que les méridiens (les arcs Nord-Sud) deviennent parallèles. A la fin, si vous avez projeté le globe terrestre tel qu'il est en réalité (et qui n'est donc pas celui que connaissait Ptolémée), vous aurez une carte très trompeuse, sur laquelle, par exemple :

_ le Groenland semblera plus grand que l'Amérique latine, alors qu'il est 6 fois plus petit ;

_ ce même Groenland semblera de même taille que l'Afrique... qui est portant 15 fois plus grande que lui !

_ la Russie semblera beaucoup plus grande que l'Afrique... alors que celle-ci est plus grande que l'Inde, l'Europe, la Chine, le Japon et les Etats-Unis réunis !

_ l'Antarctique apparaîtra comme le plus grand continent... alors qu'il est l'avant-dernier (devant l'Australie), etc.

Ce serait, évidemment n'importe quoi ; on comprend que Ptolémée n'ait pas voulu d'un système de ce genre pour représenter le monde. Mais on est alors confronté au fait que cette méthode de projection... est bien celle qui est au fondement de notre représentation actuelle du globe terrestre, qui repose sur la projection cylidrique adoptée par Mercator au XVI° siècle. A quoi ressemble en effet cette carte du monde "invraisemblable" obtenue par projection cylindrique, à l'aide d'un cylindre de Mercator ?

A ça :

Et, en plus gros, à ça :

Vous la connaissez ? C'est normal : c'est celle qui est affichée dans les salles de classe, celle que l'on trouve au Ministère des Affaires étrangères, ou à l'ONU, ou même dans les parutions de Médecins sans Frontières !... Une carte extrêmement "valorisante", en termes d'espaces, pour le Groënland et l'Antarctique, certes... mais aussi pour l'Europe, l'Amérique du Nord et la Russie... au détriment de l'Afrique, de l'Amérique latine, ou de l'Inde. Une carte qui n'a donc rigoureusement rien de "neutre", dans la distorison qu'elle impose à notre image du monde. 

Nous reviendrons plus tard sur ces enjeux idéologiques de l'image du monde fournie par les cartographes. Pour l'instant, nous noterons seulement que, chez Ptolémée déjà, la géographie était apparue indissociable des mathématiques, et d'une démarche de géométrisation du monde. Ce lien entre cartographie et mathématiques nous indique déjà en quoi la redécouverte de Ptolémée par les Humanistes de la Renaissance et du XVII° siècle va pouvoir être mise à contribution pour le passage à une conception géométrique du monde, intégrable à une conception scientifique de la réalité.

          3. Latitude, longitude et astronomie

Et, comme nous l'avons dit, elle est également liée au domaine de l'astronomie. Pourquoi ? Tout simplement parce que, dès que la géographie est abordée dans les termes géométriques du calcul des coordonnées, il faut s'en remettre aux astres. Pour déterminer la circonférence de la Terre, Erathostène (astronome, géographe, philosophe et mathématicien grec du IIIe siècle avant JC) avait mesuré l'ombre portée d'un gnomon (bâton planté dans le sol) à Alexandrie, au moment où le soleil éclairait le fond d'un puits à Syène (Assouan).

C'est donc à partir de l'angle des rayons solaires par rapport au sol terrestre, et par des calculs mathématiques, qu'Erathostène avait pu produire son estimation de la circonférence terrestre, qui nous étonne aujourd'hui encore (il proposa 39 375 km ; la longueur exacte est de 40 075 km...) Cette articulation des mesures terrestres et de l'observation céleste se poursuivra et s'approfondira au cours de la Révolution cartographique : car pour déterminer la latitude d'un point, c'est vers les astres qu'il faut lever les yeux (par exemple en mesurant la hauteur de l'étoile polaire au-dessus de l'horizon). Comme l'illustre le dessin suivant, on voit que, plus on monte vers le Nord, et plus l'étoile polaire sera "haute" au-dessus de l'horizon (et donc : plus l'angle qu'elle forme avec le pôle sera ouvert).

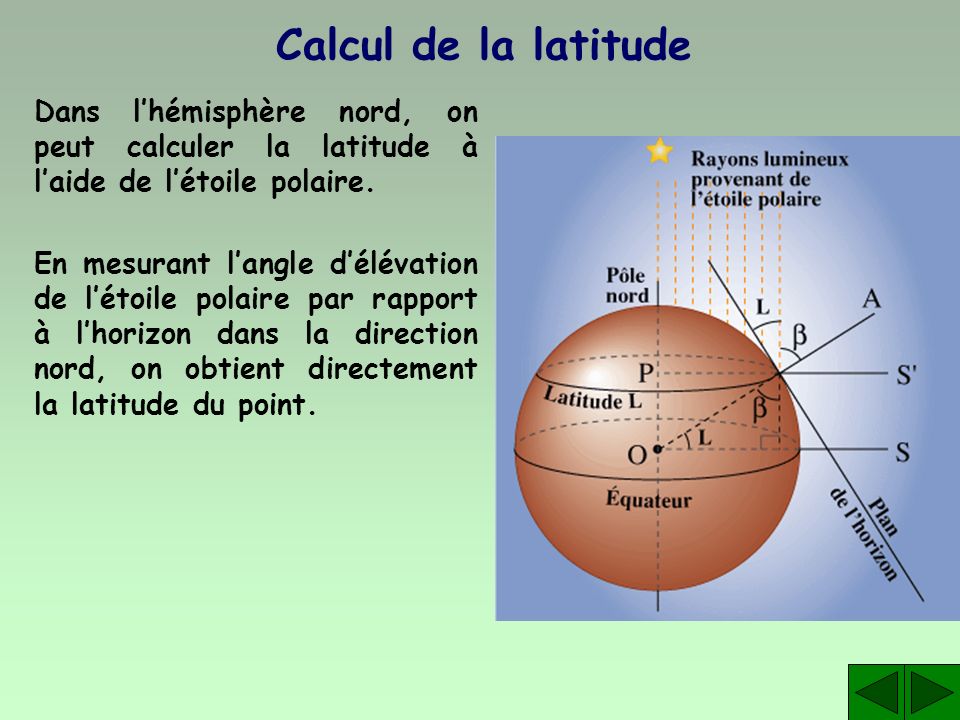
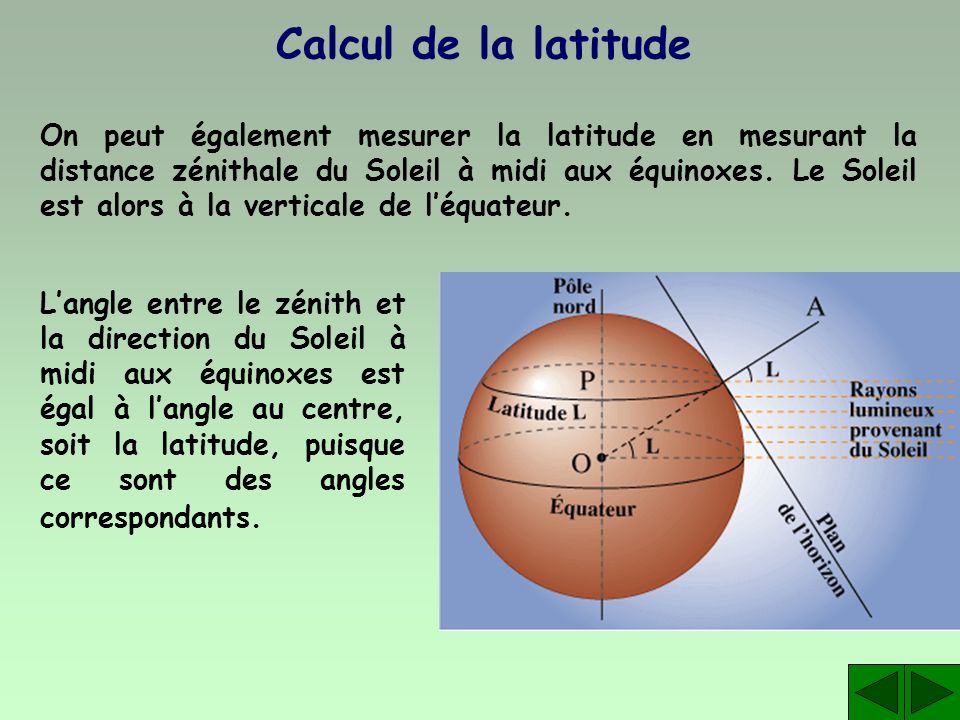
Il va de soi que cette technique n'est pas très pratique dans l'hémisphère Sud... où l'on ne voit même plus l'étoile polaire. On pourra alors tenter une autre méthode, qui repose sur la position du Soleil aux équinoxes. On sait que lors des équinoxes, à midi, le Soleil est à la verticale de l'équateur ; en mesurant son écart par rapport à la verticale à midi lors d'une équinoxe, on peut donc mesurer la distance à laquelle on se trouve de l'équateur :

[Pour information  j'ai extrait les deux images précédentes du site d'un prof de mathématiques, André Ross, qui regorge d'illustrations simples et claires pour le rapport entre astronomie et géographie depuis l'Antiquité : vous le retrouverez en cliquant sur l'image ci-dessus.]

Et en ce qui concerne la longitude, ce sont encore les astres qui serviront de repères (par exemple... les lunes de Jupiter découvertes par Galilée !), avant que le chronomètre de marine puisse prendre la relève au XVIII° siècle. Tout au long de la renaissance et de l'Âge classique, les mesures géographiques sont avant tout des mesures astronomiques : c'est l'observation du ciel qui permet de mesurer la terre, de déterminer les coordonnées géométriques des lieux sur sa surface.

     C. Géographie et astronomie : la double géométrisation

C'est donc la géométrisation de la géographie (par un "retour à Ptolémée") qui implique son rattachement à l'astronomie au cours de l'âge classique ; or nous avons vu que le propre de la Révolution astronomique était de conduire à une géométrisation de l'image de l'Univers au cours du XVII° siècle (en rupture, cette fois, avec l'image ptoléméenne de l'Univers). Au cours de la révolution cartographique, une géographie en voie de géométrisation va donc se rattacher à une astronomie qui, elle-même, est en voie de géométrisation : l'articulation des deux produira un moteur puissant dans la géométrisation de l'image du monde, conçu à la fois comme monde céleste et monde terrestre, dans l'espace unifié des traités "de la Sphère"

Ce lien entre cartographie, astronomie et mathématiques nous indique donc en quoi la révolution cartographique, articulée à la révolution astronomique, va participer à cette transformation que constitue le passage à une conception géométrique du monde, intégrable à une conception scientifique de la réalité. Quiconque voudra aborder un peu sérieusement les rivages de la géographie humaniste devra s'armer des outils du géomètre, et d'une solide formation en astronomie et en mathématiques.

Gerard Dou – L’Astronome à la chandelle, 1665

Ici encore, le domaine des Humanités nous renvoie donc à un espace devenu inhabituel, où l'on ne saurait dissocier l'étude des textes antique (philologie), les mathématiques et les configurations astrales. La Révolution cartographique appartient autant au domaine de la géographie et de la cartographie, qu'à celui de la philologie et de la philosophie, à celui du calcul et de la géométrie, ou encore celui des sciences en général. Elle engage l'ensemble de cette constellation culturelle qu'on appelle "Humanités".

Rien d'étonnant, donc, à ce que cette "révolution cartographique" soit liée à l'émergence et au développement de ce courant fondamental de la Renaissance et de l'Âge classique qu'est l'Humanisme.

Erasme, par Holbein le jeune (vers 1530)