Perspective et géométrisation

Perspective et géométrisation du monde

Le premier élément de réponse nous est déjà familier ; si nous considérons que le passage à la représentation en perspective est essentiellement un phénomène qui se produit à Florence, entre 1420 et 1450, on doit souligner que ce mode de représentation est intimement lié à l'adoption d'une vision géométrique du monde, et donc à une représentation géométrisée de la réalité. La perspective florentine... c'est de la géométrie appliquée (il existe un autre foyer d'émergence de la perspective, dans les Flandres, qui, lui, ne repose pas sur une géométrisation). 

Si les peintres forment des images du monde fondées sur des principes géométriques, c'est donc que la "géométrisation du monde" est déjà à l'oeuvre. Les principes mathématiques que le peintre établit sous forme de principes théoriques, ne sont pas pour lui de simples "conventions" que l'homme choisit arbitrairement : ce sont les principes qui structurent la réalité elle-même. Les lois que le peintre doit suivre pour déterminer l'élévation du point de fuite, et ensuite déterminer le bon écartement des parallèles, sont des lois qui s'imposent à lui du fait des principes de l'optique, qui sont eux-mêmes des principes géométriques.

Une belle perspective linéaire monofocale : le Pérugin, Christ remettant les clés à saint Pierre , 1481

Il ne s'agit pas encore, au 15e siècle, d'établir les lois de l'optique moderne, comme les lois de la refraction qui permettent de comprendre ce qu'il se passe dans une lentille (et dans l'oeil) ; ces lois, nous l'avons dit, ne seront établies que par Kepler au XVII° siècle. La théorie optique sur laquelle prennent appui les peintres du Quattrocento consiste essentiellement dans le fait de considérer la vision comme un processus dans lequel des rayons lumineux convergent, depuis les objets, vers l'oeil qui les perçoit, formant ainsi une "pyramide visuelle".

La pyramide visuelle illustrée par Alberti, le grand théoricien italien de la perspective

Dans cette optique, le tableau n'est plus considéré comme une surface que l'on doit peindre, mais bien comme une surface interposée entre l'objet représenté et l'oeil : le tableau devient une "fenêtre", qui représente ce que le spectateur verrait si les objets représentés existaient réellement. Il faut ici faire attention : ce n'est pas le monde que le peintre doit représenter : le tabeau n'est pas une fenêtre "sur le monde" ; mais bien, selon Alberti  une fenêtre sur l'histoire. On pourrait ainsi dire que le tableau "donne sur" des mondes qui sont une créatrion de l'esprit du peintre, mais d'une façon telle que le tableau les fait apparaître tels que le spectateur les verrait s'il était en train de les observer.

Construire une bonne représentation, c'est donc être capable de déterminer exactement ce que serait l'image visuelle perçue par l'oeil du spectateur, qui contemplerait la scène représentée depuis un certain point de vue. Et le seul moyen de produire cette image exacte, c'est de déterminer mathématiquement la forme que prendrait l'objet du fait de sa distance et de son élévation par rapport à l'oeil qui le regarde. C'est bien une procédure géométrique que doit suivre le peintre.

Une illustration contemporaine des rapports entre arts graphiques et géométrie : Thomas Canto

Quand nous parlons de "la perspective", nous désignons en fait un type particulier de représentation en perspective : nous parlons principalement de la perspective linéaire monofocale. Ce type de représentation correspond à l'image qui est vue par un oeil, unique et immobile, situé en un point p. Ce mode de représentation nous est tout à fait familier... puisque c'est celui que nous retrouvons dans la photographie et le cinéma. Les images (sauf trucage) qui s'impriment sur la pellicule (du temps, du moins, où il y avait des pellicules) sont celles qui sont restituées par une lentille qui joue un rôle analogue à celui d'un oeil humain immobile.

Dans cette optique (au sens propre), les dimensions des objets rétrécissent avec la distance, conformément à un principe simple : les parallèles équidistantes dans la réalité se rapprochent, qu'elles soient horizontales ou verticales.

Pour illustrer ce principe bien connu, supposons que vous soyez face à une pièce dont les murs sont recouverts d'un papier peint rayé : sur le fond blanc, des lignes noires sont tracées, à distance régulière. Si les murs, le sol et le plafond sont tapissés, la vision en perspective fera apparaître un "rapprochement" progressif des lignes, aussi bien horizontales (sol et plafond) que verticales (mur).

La conséquence de ce "rapprochement", c'est bien sûr que les lignes parallèles orientées vers le fond convergent dans l'image : toutes les lignes du sol, si on les prolonge, tendent à converger vers un point unique sur l'image. C'est aussi le cas de toutes les lignes des murs orientées vers le fond. Comme c'est aussi le cas des lignes du plafond. Et ce qui est fascinant, c'est que toutes ces lignes convergent.... vers le même point, que l'on appelle "point de fuite". C'est ce qu'illustre le dessin ci-dessous :

Si on applique ce principe à la représentation d'un paysage réel (disons : une route en ligne droite), cela donne ce genre de choses :

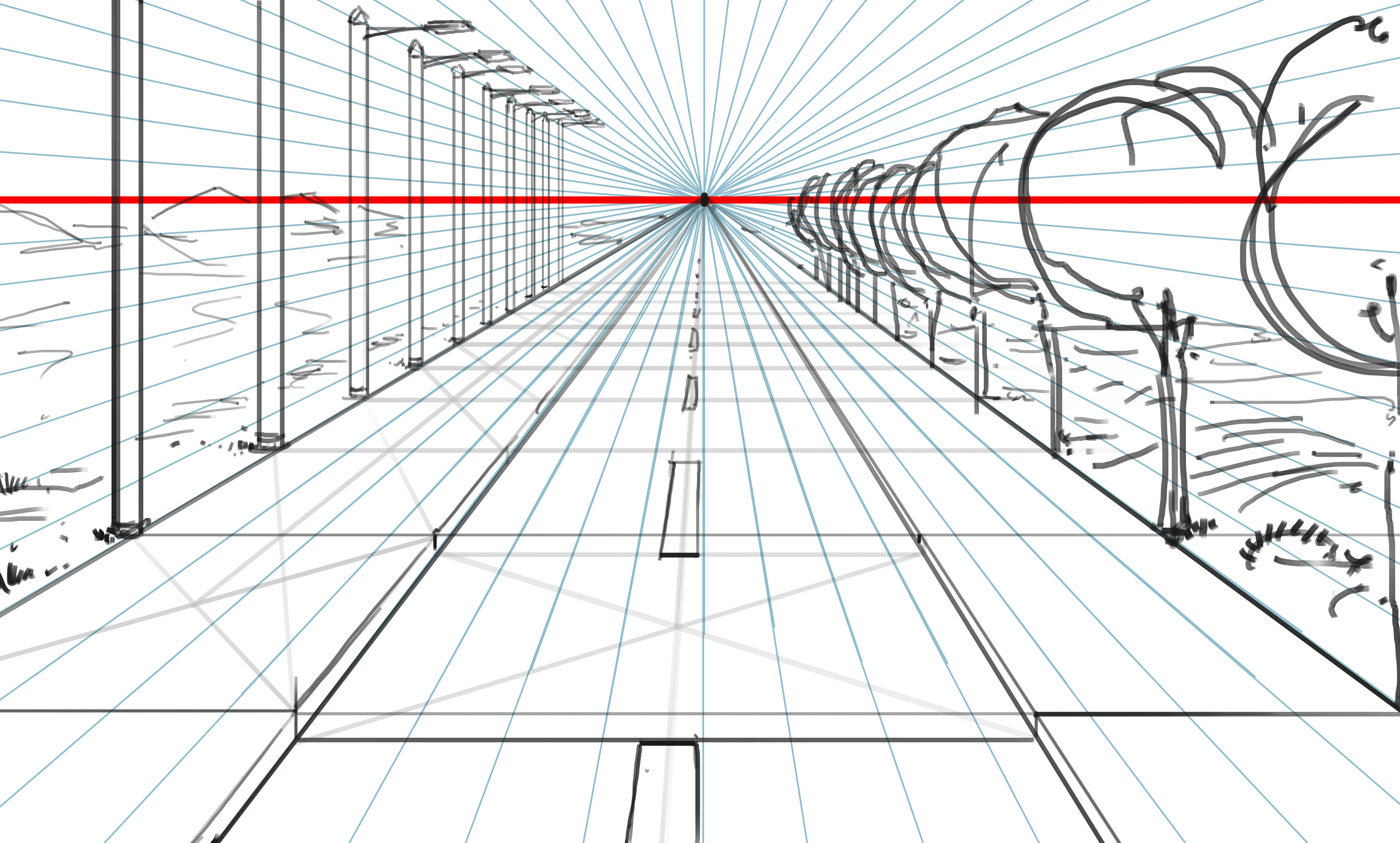
La ligne rouge (qui constitue la ligne de "rencontre" entre les lignes de ciel et les lignes de terre : c'est l'horizontale qui passe par le "point de fuite") est la "ligne de fuite". Tout photographe a un jour pris une photo de ce genre, surtout s'il est allé aux Etats-Unis : la ligne de fuite et le point de fuite apparaissent avec évidence.

Et c'est encore mieux quand on prend une voie de chemin de fer, car on voit nettemment le rapprochement (mais non la convergence) des parallèles horizontales, correspondant aux traverses de la voie.

Les vues de ville (et notamment des grandes villes contemporaines) se prêtent particulièrement bien à ce type de représentation, du fait de l'entrelacement des horizontales et des verticales, qui fait apparaître la convergence des parallèles vers le point de fuite :

Ou, en moins schématique :

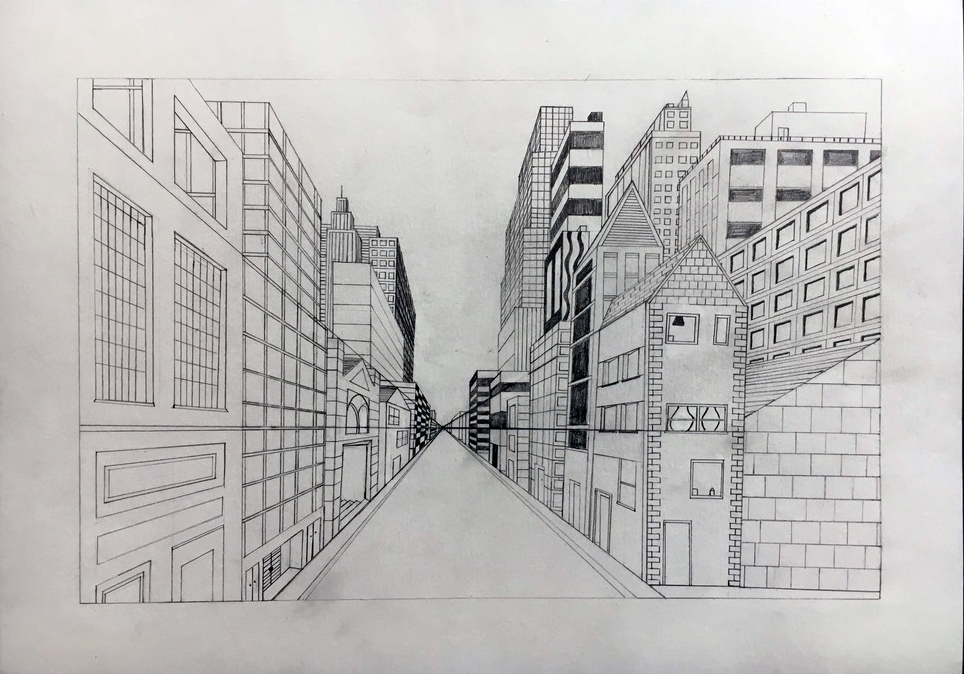
Toutes ces images correspondent à une représentation en perspective linéaire (les parallèles sont représentées par des droites) monofocale (il n'y a qu'un point de fuite). Encore une fois, il faut insister sur le fait qu'il s'agit d'un choix, qui n'a rien de nécessaire. Non seulement rien n'impose une représentation "en perspective", mais même dans les représentations en perspective, celle-ci n'est qu'une possibilité parmi d'autres.

Si elle accède à la dominatiin en Italie au Quattrocento, c'est parce qu'elle satisfait pleinement l'exigence géométrique, aussi bien dans sa dimension théorique que dans sa dimension pratique. Ce sont des procédés géomériques qui vont donner au peintre les moyens techniques permettant de construire son oeuvre. Le peintre rejoint ainsi l'architcte, qui fonde ses constructions sur des principes mathématiques. En ce sens, ce n'est pas un hasard si celui que l'on considère comme "l'inventeur" de la perspective, Filippo Brunelleschi, auteur à la fois du premier tableau en perspective linéaire monofocale et du dispositif technique permettant d'en vérifier l'exactitude est un architecte. Le but de Brunelleschi reste d'ailleurs l'objet de discussion ;: mais il est assez probable que le but de son dispositif n'était pas de permettre la création d'oeuvres d'art, mais bien de démontrer qu'il était possible pour les architectes de substituer une oeuvre peinte au traditionnel modello, cette maquette préparatoire de la construction.

Le dispositif de Brunelleschi fait partie des "lieux comuns" sacrés de l'histoire de la peinture. Vous en trouverez sans difficulté des dizaines de description : je n'en rappelle que le principe, qui est de percer un trou circulaire à l'endroit du point de fuite du tableau, puis de se replacer devant la scène représentée en tenant devant soi un miroir : en faisant bouger le miroir, en peut vérifier que la similitude entre ce que l'oeil voit "en vrai" et ce qu'il voit dans le miroir (qui reflète le tableau) est parfaite.

La tavoletta de Brunelleschi (et le tableau peint) ont été perdus... mais on en a reconstruits depuis !

Reste que si ce dispositif, qui date de 1415, nous éclaire sur la nature de la perspective, et démontre son efficacité, elle ne nous dit pas comment on doit s'y prendre pour peindre l'image qui se reflètera dans le miroir. Où situer le point de fuite ? Comment déterminer le rapprochement des parallèles ? C'est bien grâce à des considérations et des procédés géométriques que le peintre florentin va pouvoir répondre à ces questions.

Pour savoir où situer le point de fuite, le peintre doit d'abord la hauteur par rapport au sol de l'oeil censé contempler la scène représentée. Le point de fuite se situe au centre de la vision d'un oeil qui regarde devant lui. La hauteur du point de fuite sur le tableau est donc déterminée par la hauteur du regard par rapport aux objets du tableau, mais aussi par l'emplacement et les dimensions de la "fenêtre" du tableau.

Prenons le cas le plus simple : une toile qui est posée sur le sol, et qui représente ce que perçoit un oeil situe à environ 1.75 du sol, qui regarde droit devant lui. La ligne de fuite sera située à 1.75 du sol. Si la toile ne va pas jusqu'au sol, il faut évidemment diminuer la hauteur du point de fuite par rapport au bas du tableau. Si l'oeil regarde vers le bas, il faut élever le point de fuite, ; et s'il regarde vers la gauche, il faut décaler le point de fuite vers la droite, etc. Impossible de s'en sortir si l'on ne dresse pas dès le départ un schéma permettant de situer l'oeil, la scène représentée et l'emplacement de la toile.

Et les choses deviennent plus compliquées pour déterminer la position des parallèles, et leur rapprochement au fur et à mesure qu'elles "s'éloignent" en direction du point de fuite. Reprenons le cas où je représente ce que voit un oeil qui regarde une pièce dont les papiers peints sont rayés par des lignes régulières. Une fois situé mon point de fuite, je sais comment faire converger les lignes parallèles du sol orientées vers le fond : il suffit de "tirer" mes lignes depuis le point de fuite.

Mais comment placer les perpendiculaires ? A quelle hauteur dois-je situer les lignes horizontales du sol, du plafond ? Quel espacement dois-je prévoir entre les lignes verricales des murs ? et quelle diminution dois-je effectuer ?

Prenons un exemple simple : si je dois représenter une cuisine vue par homme "normal", cuisine dont le sol et les murs sont carrelés. Où dois-je tirer les "traits" horizontaux qui correspondent aux carreaux du sol ? les traits verticaux qui correspondent à ceux des murs ?

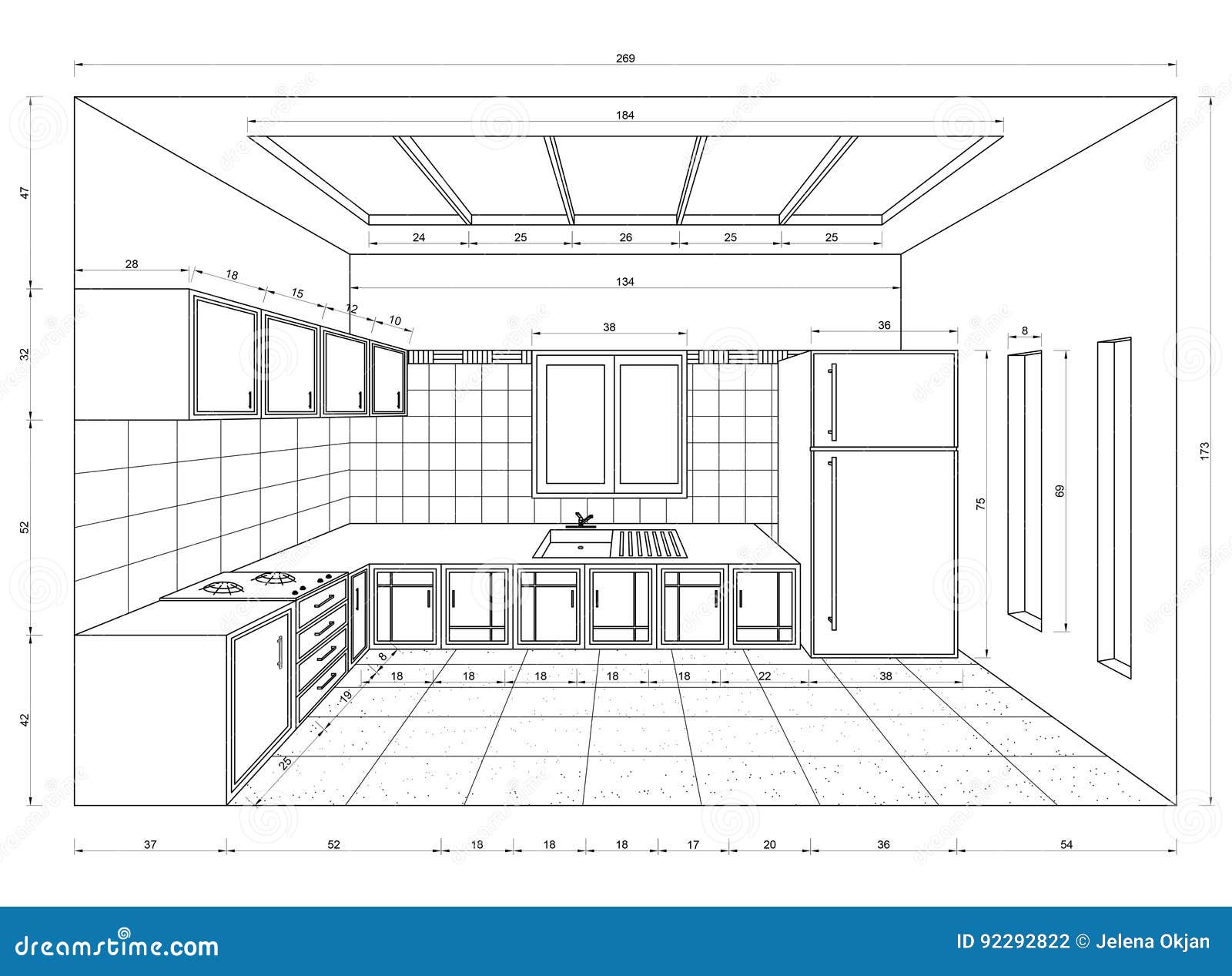Le

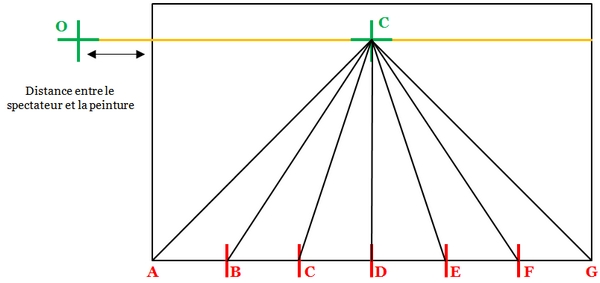
Le moyen le plus simple dans cette situation est de placer, à côté de ma feuille, une seconde feuille, sur laquelle je ferai apparaître une seconde "pyramide visuelle", correspondant à la vision d'un spectateur observant la même scène, à la même hauteur, à la même distance, mais de façon latérale. Concrètement, je construis une seconde "pyramide visuelle", dont l'origine est un point dont la distance au "point de fuite" (distance OC) correspond à la distance de l'oeil au tableau :

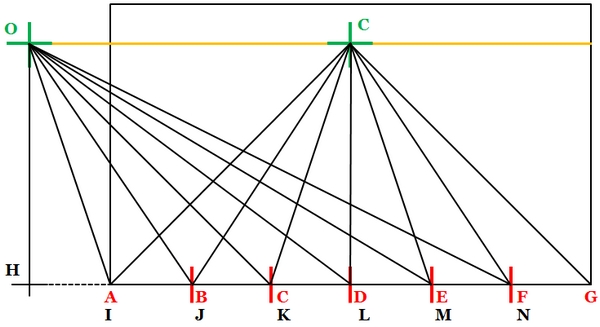
Les deux réseaux de ligne se croisent : les lignes "tirées" depuis O coupent les lignes "tirées" depuis C ; et les points d'intersection se situent en fait sur les lignes que je cherche. On voit en effet que les points d'intersection sont bien situés sur des droites, que je n'ai plus qu'à tracer.

ou encore :

Plus encore, je n'ai pas besoin de trouver tous mes points d'intersection : un petit nombre suffit. Car non seulement un point d'intersection m'indique toute la droite parallèle qui passe par ce point (et qui, de fait, si j'ai été rigoureux, passera par tous les autres points d'intersection), mais de plus, une fois tracée ma première ligne horizontale, il me suffit de tracer les diagonales (correspondant ci-dessus aux lignes turquoises) pour trouver d'autres ppints d'intersection. C'est ce qui explique que, sur la plupart des dessins préparatoires en perspective, sur un sol en damier figure systématiquement les "diagonales", qui permettent de trouver et / ou de vérifier l'écartement des parallèles transversales (c'est le cas dans les deux illustrations suivantes).

Cela, c'est le principe. Avec un peu d'habitude, cela va très vite, et un enfant de 8 ans y arrivera (j'ai essayé).

Il y arrivera... du moins tant qu'il s'en tiendra à un espace carrelé avec des carreaux carrés, vu de face, tous orientés de la même façon, à hauteur d'homme. Car dès que l'on fait intervenir des objets qui ne sont pas carrés, cubiques ou parallélépipédiques ; dès qu'ils sont orientés différemment au sein du même espace ; dès que les choses sont perçues de biais, ou de haut, etc. les choses deviennent beaucoup, beaucoup plus compliquées.

On peut compliquer en faisant intervenir des formes circulaires, comme des arches, des ogives, ce genre de choses...

Et c'est encore plus amusant quand on ajoute la variation de l'orientation des objets dans l'espace :

Il peut bien sûr être tentant d'opter ensuite pour des perspectives plongeantes, voire délibérément "penchées"...

...mais il va de soi que, avant d'arriver à le faire, il va falloir intégrer parfaitement les principes géométriques de la représentation !

Nous l'avons dit : ce mode de représentation n'est pas plus "vrai" que d'autres ; c'est d'ailleurs ce qui explique qu'il ait pu être rapidement remis en cause, au moins en partie, par les peintres de la Renaissance. Léonard de Vinci maîtrisait parfaitement les principes géométriques de la représentation en perspective linéaire monofocale ; il s'en est pourtant affranchi (aucun tableau de Léonard ne respecte ces principes après la fameuse Cène), pour s'orienter vers d'autres recherches, portant notamment sur le jeu des couleurs. Les couleurs, en effet, s'estompent avec la distance, de même que les contours deviennent moins nets : c'est sur ce double registre que jouent les dernières peintures de léonard pour faire apparaître la profondeur. Pour Léonard, la perspective pouvait être un moyen, elle ne constituait jamais une fin en soi : c'est ce qui explique que, même losrque les travaux préparatoires font apparaître la structuration géométrique de l'espace, le tableau final tend à sacrifier la structure mathématique au profit d'une "matière" visuelle, de formes et de couleurs qui lui échappent.

A cet égard, le tableau (inachevé) intitulé L'adoration des mages est instructif. Une première esquisse ne s'embarrasse pas de considérations géométriques : il y a bien une perspective, mais elle est (très) loin de respecter des principes rigoureux, garantissant la cohérence géométrique de l'ensemble :

Dans un deuxième temps, Léonard procède à la structuration géométrique de la représentation : on voit apparaître les lignes de fuite, le dessin des structures architecturales (comme l'escalier) est soumis au système d'ensemble, convergent vers le point de fuite, etc.

On pourrait dès lors s'attendre à ce que le tableau final, même inachevé, respecte ce bel ordonnancement géométrique de l'espace. Mais ce n'est pas le cas : le tableau est dévoré par un premier plan au sein duquel la perspective disparaît (le "dallage" géométrique est explicitement masqué par un sol qui s'apparente à un drapé), et par un espace latéral où un combat de cavaliers (dont on peut d'ailleurs se demander ce qu'il vient faire là) s'affranchit également des contraintes de la géométrie.

On voit que, pour Vinci, la "validité" géométrique de la représentation ne constutuait pas le critère de sa valeur. Il y a bien une volonté de vérité chez Léonard, mais cette vérité n'équivaut pas à une obéissance stricte aux principes géométriques de la perspective. Léonard n'est certainement pas un "anarchiste" de la peinture, pronant le sacrifice des règles au profit de l'expressivité. Il accepte tout à fait le principe selon lequel plusieurs lieux ne peuvent pas être représentés sur la même image, et il est l'un des premiers à avoir insisté sur le fait qu'un même personnage ne pouvait pas être représenté plusieurs fois sur le même tableau. Il applique donc scrupuleusement les principes qu'Aristote avait énoncés pour la tragédie : unité de lieu, unité de temps, unité d'action. S'il rejette la perspective, c'est qu'elle lui semble artificielle (et non naturelle) ce qu'elle est effectivement : pour être véritablement valide, une peinture en perspective linéaire monofocale exigerait un spectateur doté d'un oeil unique (c'est rare), parfaitement immobile (ce n'est jamais le cas), placé à un endroit exact (déterminé par l'emplacement du point de fuite et la distance au tableau impliquée par la représentation).

Donc : pour Léonard de Vinci, la représentation en perspective linéaire monofocale, fondée sur les principes géométriques de l'optique, n'avait pas le privilège de la vérité. Mais Léonard s'opposait ainsi (consciemment) aux maîtres de la perspective florentine, et notamment au traité d'Alberti, selon lesquels cette perspective constituait bel et bien la perspective légitime (c'est d'ailleurs le nom qu'ils lui donnaient). Pour Alberti, respecter la structure géométrique de la représentation, c'était respecter les principes mathématiques inscrits dans la réalité même : c'était soumettre l'image du monde aux lois du monde lui-même, telles que Dieu les avait prescrites. Plus encore : Alberti savait très bien que la perspective linéaire monofocale ne correspondait pas exactement à la manière dont nous regardons habituellement le monde (nous avons deux yeux, qui sont en mouvement, les couleurs s'estompent, les contours se brouillent, etc.) : mais justement, le tableau permettait de corriger les imperfections de la vue ordinaire : elle montrait le monde tel qu'il devait être vu pour que sa structure interne, les lois géométriques prescrites par Dieu, apparaissent pleinement.

Les peintres florentins du Quattrocento qui ont inventé la perspective considéraient donc bien, eux, qu'ils la découvraient : qu'ils dévoilaient ainsi un ordre naturel, vrai, inscrit dans la structure même du monde tel que Dieu l'a conçu. La représentation du monde en perspective traduisait donc bien une certaine perspective sur le monde : la géométrisation de la représentation exprimait bien la géométrisation de l'image que les peintres florentins se faisaient de la réalité.

Une peinture géométrique du monde traduit la vision d'un peintre qui considère que le monde a été créé par un Dieu géomètre.